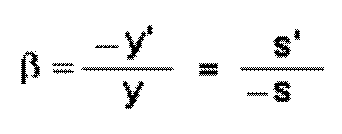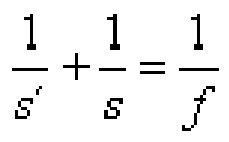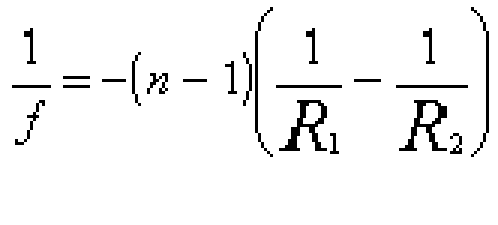Las lentes son medios transparentes limitados por dos superficies, siendo curva al menos una de ellas.
Las lentes con superficies de radios de curvatura pequeños tienen distancias focales cortas. Una lente con dos superficies convexas siempre refractará los rayos paralelos al eje óptico de forma que converjan en un foco situado en el lado de la lente opuesto al objeto. Una superficie de lente cóncava desvía los rayos incidentes paralelos al eje de forma divergente; a no ser que la segunda superficie sea convexa y tenga una curvatura mayor que la primera, los rayos divergen al salir de la lente, y parecen provenir de un punto situado en el mismo lado de la lente que el objeto. Estas lentes sólo forman imágenes virtuales, reducidas y no invertidas.
Si la distancia del objeto es mayor que la distancia focal, una lente convergente forma una imagen real e invertida. Si el objeto está lo bastante alejado, la imagen será más pequeña que el objeto. Si la distancia del objeto es menor que la distancia focal de la lente, la imagen será virtual, mayor que el objeto y no invertida. En ese caso, el observador estará utilizando la lente
como una lupa o microscopio simple. El ángulo que forma en el ojo esta imagen virtual aumentada (es decir, su dimensión angular aparente) es mayor que el ángulo que formaría el objeto si se encontrara a la distancia normal de visión.
La relación de estos dos ángulos es la potencia de aumento de la lente. Una lente con una distancia focal más corta crearía una imagen virtual que formaría un ángulo mayor, por lo que su potencia de aumento sería mayor. La potencia de aumento de un sistema óptico indica cuánto parece acercar el objeto al ojo, y es diferente del aumento lateral de una cámara o telescopio, por ejemplo, donde la relación entre las dimensiones reales de la imagen real y las del objeto aumenta según aumenta la distancia focal.
La cantidad de luz que puede admitir una lente aumenta con su diámetro. Como la superficie que ocupa una imagen es proporcional al cuadrado de la distancia focal de la lente, la intensidad luminosa de la superficie de la imagen es directamente proporcional al diámetro de la lente e inversamente proporcional al cuadrado de la distancia focal. Por ejemplo, la imagen producida por una lente de 3 cm de diámetro y una distancia focal de 20 cm sería cuatro veces menos luminosa que la formada por una lente del mismo diámetro con una distancia focal de 10 cm. La relación entre la distancia focal y el diámetro efectivo de una lente es su relación focal, llamada también número f. Su inversa se conoce como abertura relativa. Dos lentes con la misma abertura relativa tienen la misma luminosidad, independientemente de sus diámetros y distancias focales.
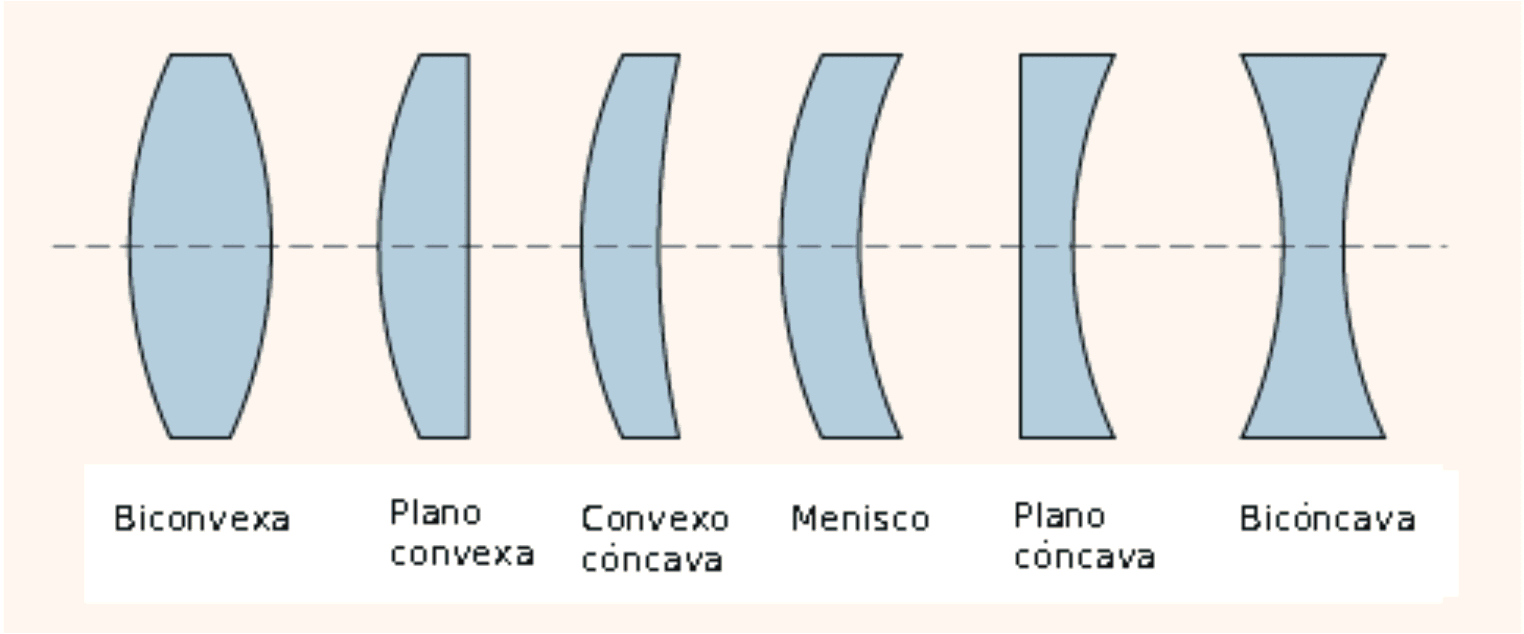
Existen dos tipos principales de lentes:
Lente convergente. Los rayos paralelos procedentes del infinito convergen sobre el plano focal imagen.
Las lentes convergentes son más gruesas por el centro que por el borde, y concentran (hacen converger) en un punto los rayos de luz que las atraviesan. A este punto se le llama foco (F) y la separación entre él y la lente se conoce como distancia focal (f).
Lentes convergentes: Son aquellas cuyo espesor va disminuyendo del centro hacia los bordes. En este tipo de lentes, todo rayo que pase paralelamente al eje principal, al refractarse se junta en su foco. Las lentes convergentes forman imágenes reales de objetos. Existen tres clases de lentes convergentes:
· Lentes bi-convexas.
· Lentes plano-convexas.
· Lentes cóncavo-convexas.
Las lentes convergentes se utilizan en muchos instrumentos ópticos y también para la corrección de la hipermetropía. Las personas hipermétropes no ven bien de cerca y tienen que alejarse los objetos. Una posible causa de la hipermetropía es el achatamiento anteroposterior del ojo que supone que las imágenes se formarían con nitidez por detrás de la retina.
Lente divergente. Los rayos procedentes de un mismo punto de un objeto divergen al atravesar la lente. Sus prolongaciones convergen a la izquierda de la lente formando formando una imagen virtual directa y reducida.
· Lentes divergentes: Son aquellas cuyo espesor va disminuyendo de los bordes hacia el centro. En este tipo de lentes, todo rayo que pase paralelamente al eje principal, al refractarse se separa como si procediera de un foco principal. Las lentes divergentes forman imágenes virtuales de los objetos. Existen tres clases de lentes divergentes:
· Lentes bi-cóncavas.
· Lentes plano-cóncavas.
· Lentes convexo-cóncavas.
La miopía puede deberse a una deformación del ojo consistente en un alargamiento anteroposterior que hace que las imágenes se formen con nitidez antes de alcanzar la retina. Los miopes no ven bien de lejos y tienden a acercarse demasiado a los objetos. Las lentes divergentes sirven para corregir este defecto.
La fórmula de las lentes delgadas permite relacionar la posición del objeto y de la imagen con
la distancia focal.
Esta es la fórmula:

Vamos a deducirla mediante relaciones geometricas sencillas. También se deduce a partir de
la fórmula del dioptrio.
En los triángulos semejantes amarillos ABO e OA’B’,
limitados por el objeto, la imagen y la lente, podemos establecer:


En los triángulos OMF’ e o F’A’B’ 

Igualando las dos relaciones:

y haciendo operaciones:

Aplicando el criterio de signos DIN (la posición del objeto a la izquierda de la lente es negativa),
la fórmula que obtenemos para las lentes delgadas es:

Aumento lateral
Aumento lateral de una lente es el cociente entre la altura de la imagen y la altura del objeto.

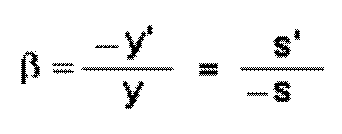
Para demostrar esta fórmula establecemos relaciones geométricas en los triángulos de la figura
siguiente:
En los triángulos semejantes BAO e OB’A’ establecemos


B’A’= y’
BA= y
Aplicando el criterio de signos DIN ( "s" e "y’ " son negativos): 
Potencia de las lentes
La potencia de una lente es la inversa de su distancia focal imagen:
 
La potencia se mide en m -1 y se conoce como dioptría.
Una dioptría es la potencia de una lente que tiene una distancia focal imagen de 1 m.
El signo de la potencia es el mismo que el de la distancia focal imagen, por lo que siguiendo las
normas DIN, la potencia de una lente convergente es positiva, P > 0.
La potencia amplificadora manifiesta la capacidad de la lente para aumentar la imagen, pero
como capacidad de aumento la del cerebro humano.
Fórmulas de Óptica Geométrica
Dioptrio esférico
Ecuación fundamental del dioptrio plano: Se obtiene a partir de la ley de Snell de la refracción y
sirve solo para rayos paraxiales.

A partir de la ecuación anterior, si hacemos s = f y s· = infinito obtenemos:
De las ecuaciones anteriores se deduce fácilmente:
 
y la denominada ecuación de Gauss:

Para rayos paraxiales se puede deducir la siguiente expresión para calcular el aumento lateral:

Dioptrio plano
El dioptrio plano lo podemos considerar como un dioptrio esférico de radio infinito. Si en la
ecuación fundamental del dioptrio esférico sustituimos R por infinito nos queda:

De donde se puede deducir fácilmente que ML= 1, es decir la imagen es del mismo tamaño
que el objeto.
Espejos esféricos
La reflexión puede considerarse como un caso particular de la refracción en el que n·= -n,
aplicando eso a la ecuación fundamental del dioptrio esférico se obtiene:

A partir de la ecuación anterior, si hacemos s·= f· y s = infinito obtenemos:

A partir de la ecuación anterior, si hacemos s = f y s· = infinito obtenemos:

Es decir f = f·= R/2
De las expresiones anteriores se deduce:
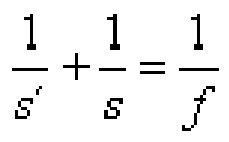
Y si a la ecuación del aumento de los dioptrios esfØricos aplicamos que n = -n· obtenemos:

Lentes delgadas
Para las lentes delgadas y para los rayos paraxiales, aplicando la ecuación fundamental del
dioptrio dos veces, se puede deducir:

A partir de la ecuación anterior, si hacemos s·= f· y s = infinito obtenemos:

A partir de la ecuación anterior, si hacemos s = f y s· = infinito obtenemos:
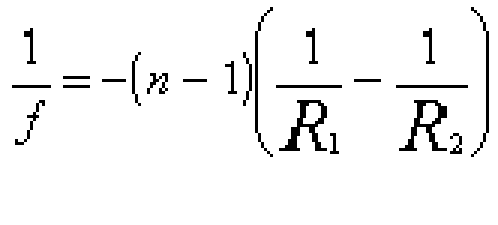
Es decir f = -f·
De las expresiones anteriores se deduce:

Y para el aumento lateral se puede deducir:

Potencia de una lente: P = 1/f· (Se mide en m-1, dioptrías)
|